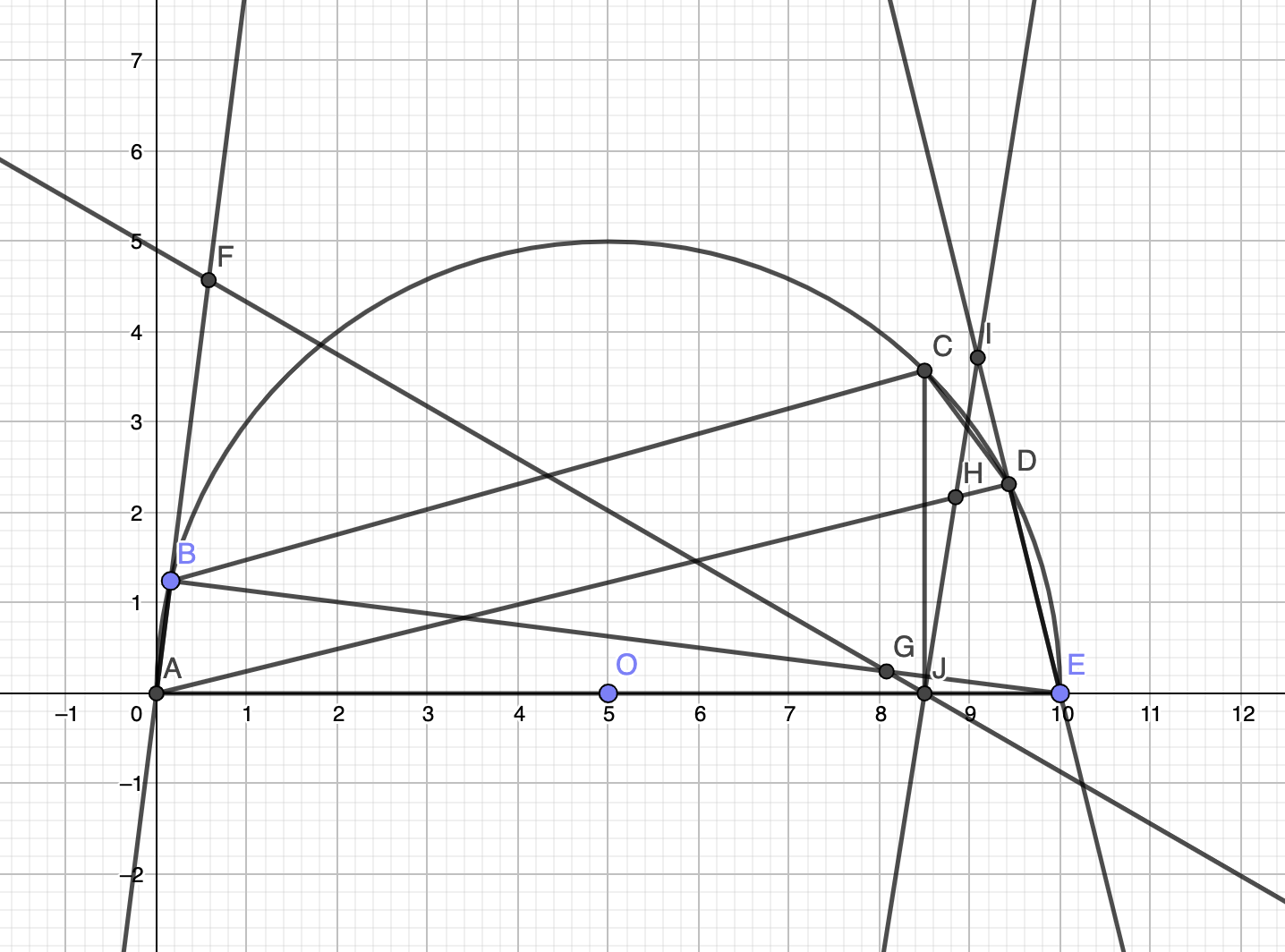
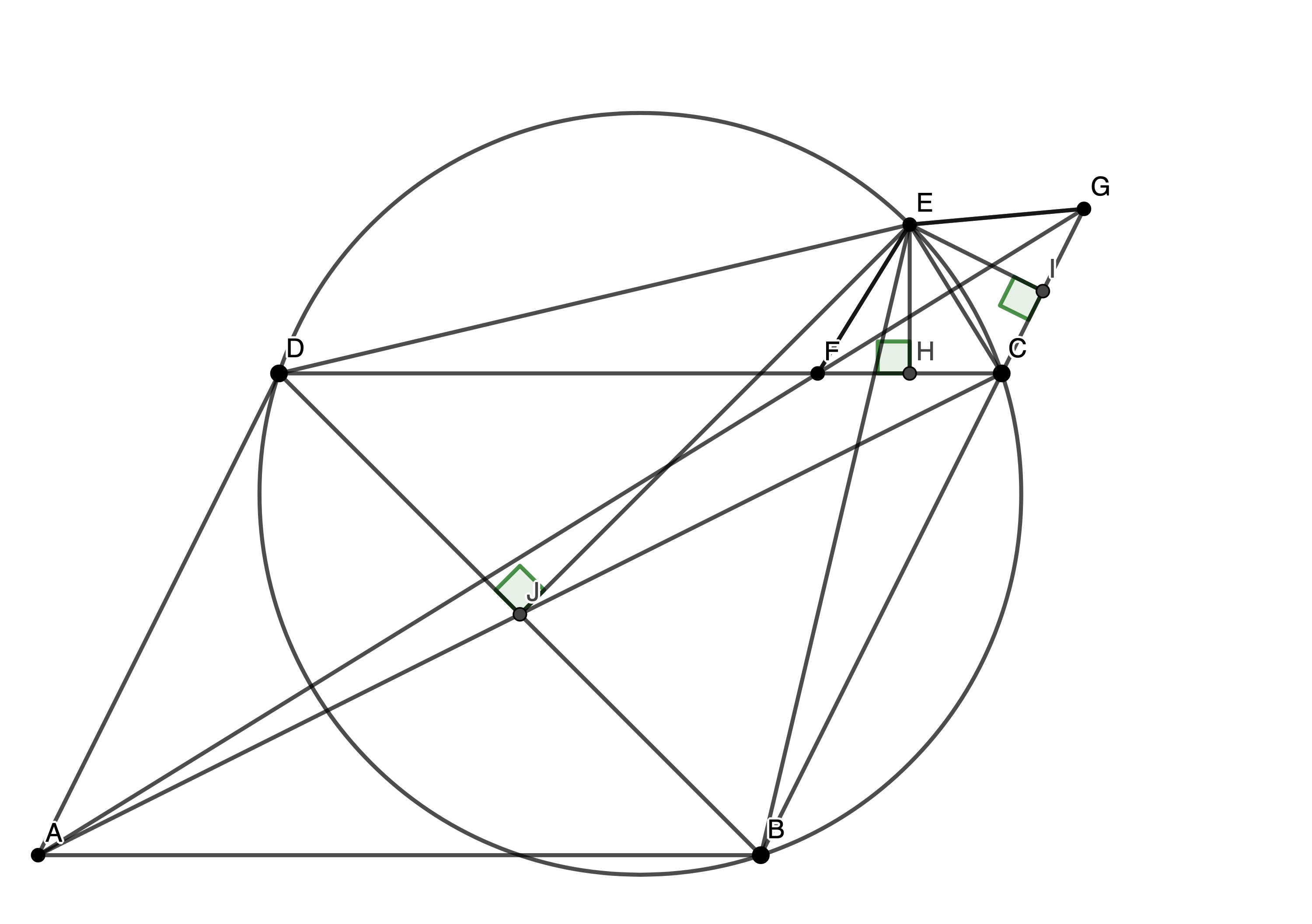
We have a cyclic pentagon, such that AE is a diameter and equals 10. We know and . Now F, G, H, I are the feet of the perpendiculars from C to AB, EB, AD, ED. If FG and HI concur at J, find FJI. Now, let K be the foot of the perpendicular from […]
Category: Synthetic Geometry
IMO 2007/2
Consider five points A, B, C, D, E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that EF = EG = EC. Prove […]
Shortlist 2001/G1
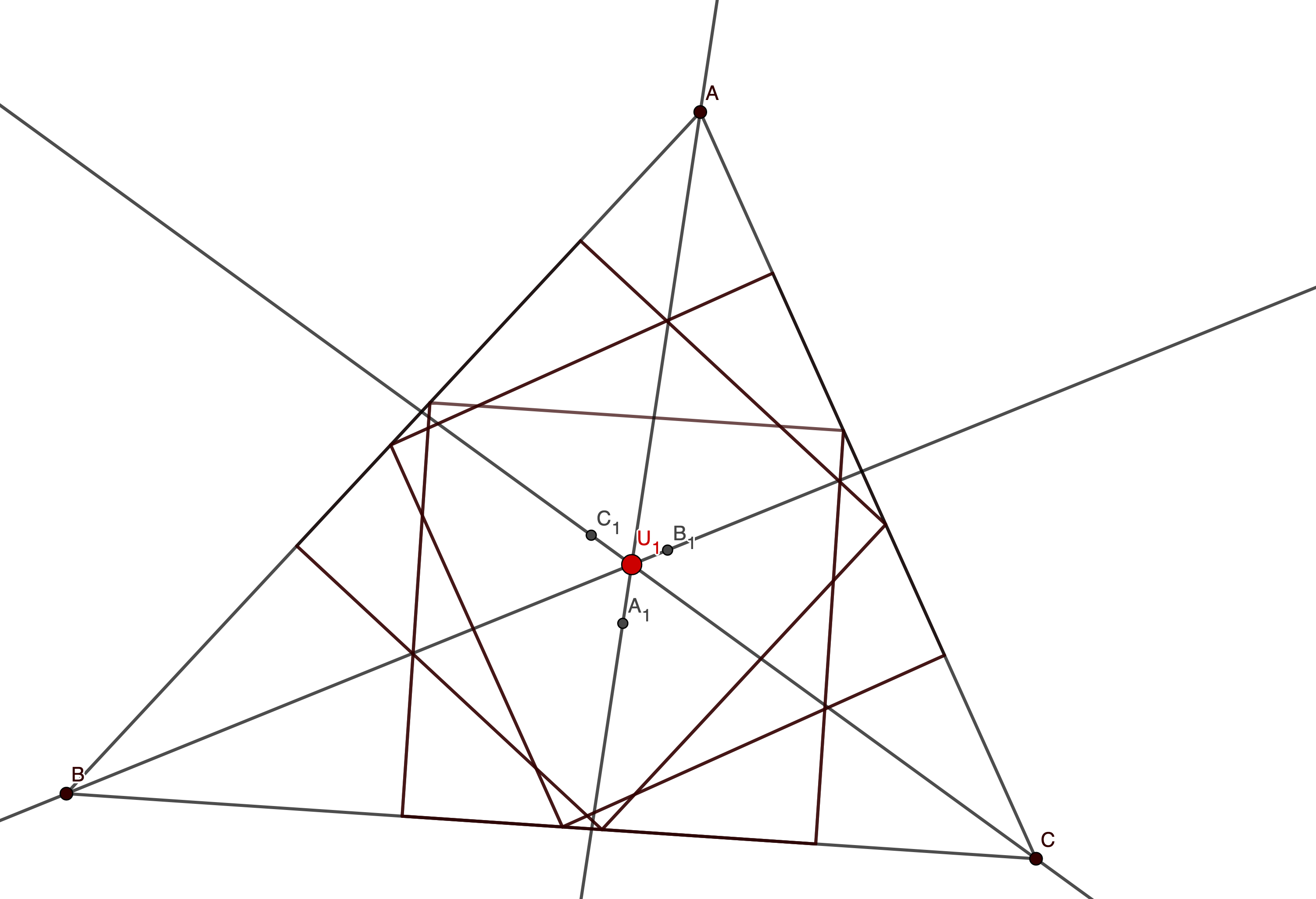
Let be the center of the square inscribed in acute triangle ABC with two vertices of the square on side BC. Thus one of the two remaining vertices of the square is on side AB and the other is on side BC. Points and are defined similarly. Prove that lines and are concurrent. The Idea […]
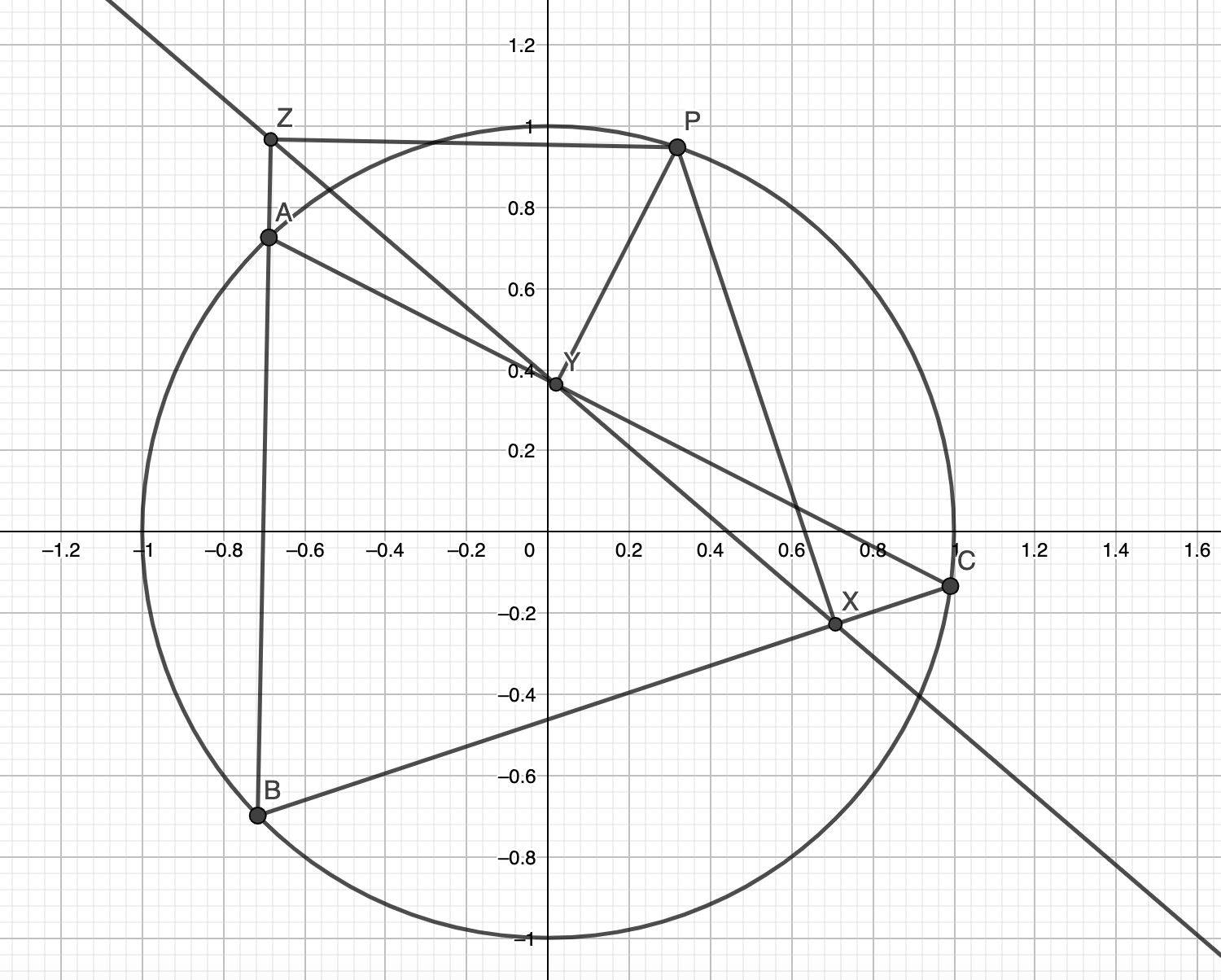
Simson Lines In USA TST
Given a point P on a triangle’s ABC’s circumcircle, then its projections on the sides of ABC are collinear (Simson Line). Using the notation from the figure above, notice that perpendiculars produce cyclic quadrilaterals: P is on the circumcircle of triangles YZA, ZXB and XYC. So we compute: due to all the cyclic quadrilaterals, and […]