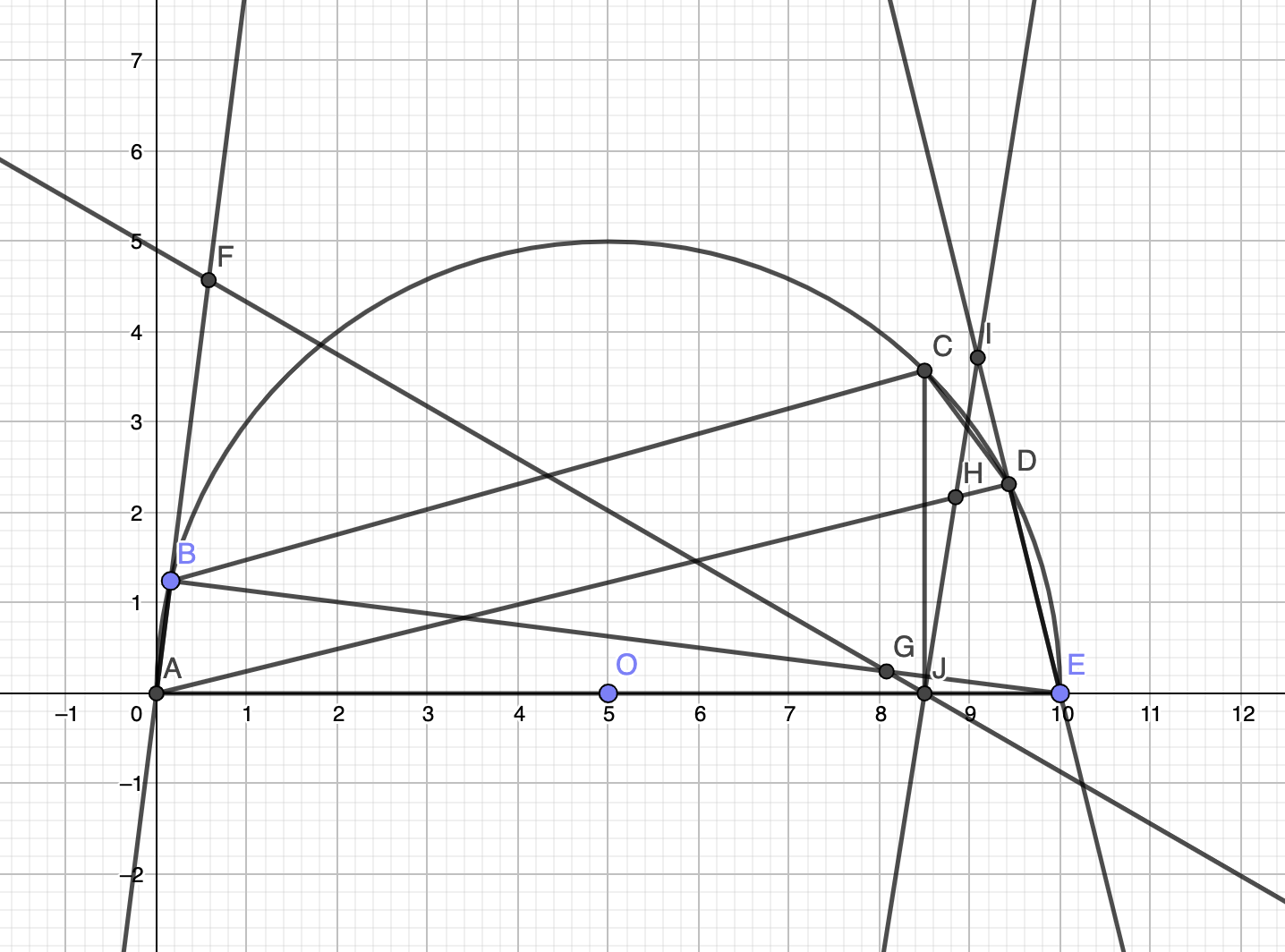
We have a cyclic pentagon, such that AE is a diameter and equals 10. We know and . Now F, G, H, I are the feet of the perpendiculars from C to AB, EB, AD, ED. If FG and HI concur at J, find FJI. Now, let K be the foot of the perpendicular from […]
Category: Uncategorized
A Problem From Stanford Mathematics Tournament 2008 (Team Test)
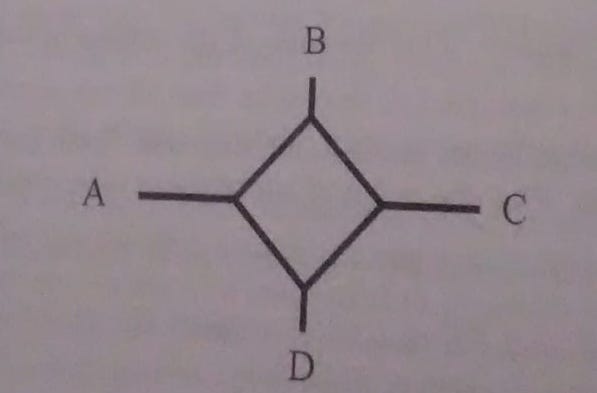
Daphne is in a maze of tunnels shown below. She enters at A, and at each intersection, chooses a direction randomly (including possibly turning around). Once Daphne reaches an exit, she will not return into the tunnels. What is the probability that she will exit at A? The Idea At first, I will denote by […]
Shortlist 2006/A5
Let be the sides of a triangle. Prove that Always Try A Substitution We notice that the denominators are all positive, in fact by the triangular inequality. So let . Then . So we get applying in the last step. Similarly, we obtain Thus, now it is sufficient to prove that So let’s assume WLOG […]