IMO 2007/2 – Mattia Giuri's bizarre blog

Consider five points A, B, C, D, E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that EF = EG = EC. Prove that l is the bisector of angle $\widehat{DAB}$ .

In this problem we’re going to exploit the collinearity of three points in to show a crucial similarity which will allow us to get the job done.

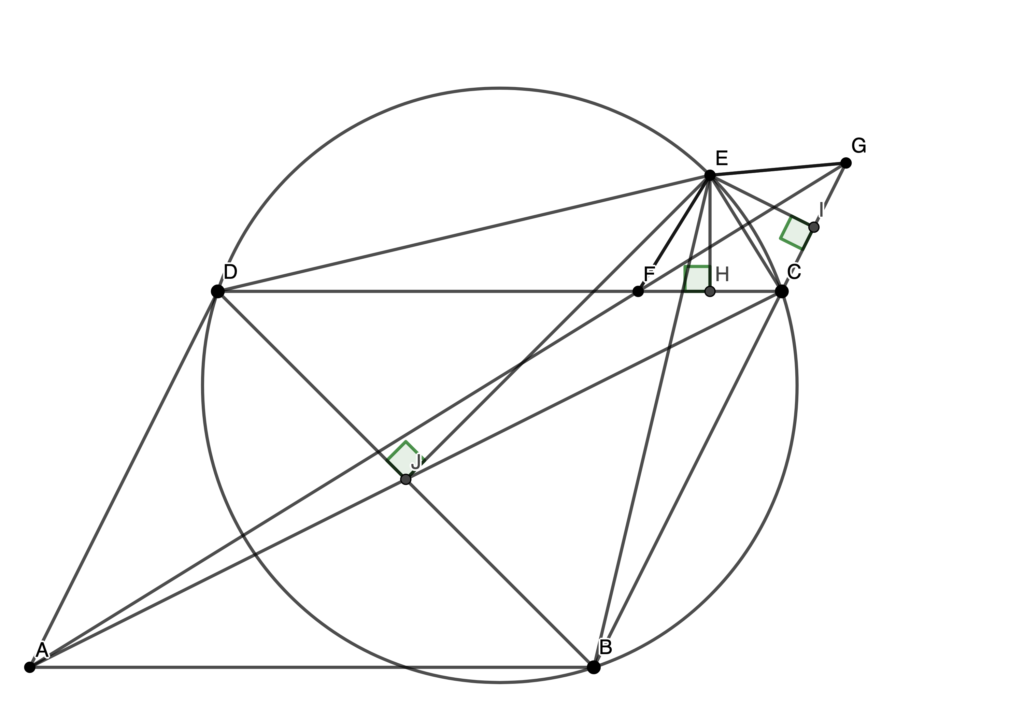
Now let’s try to use this idea in our problem. Let’s draw line AC meeting line BD at J, we all know that J is the midpoint of AC and BD. Also, let’s draw the altitudes/medians/angle bisectors of our two isosceles triangles, meeting FC and CG respectively at H, I. We notice that H, I, J are collinear by Thales theorem.

Also, they are parallel to AG because H, I are midpoints of FC, CG, so they are parallel to FG, which is AG.

Moreover, $EH \perp FC$ and $EI \perp CG$ . This means that our line is the Simson Line (see https://www.mattiagiuri.com/2020/11/19/simson-lines-in-usa-tst/) from E to triangle DBC, so we have $EJ \perp BD$ , but also BJ = JD, so EBD is hysosceles.

Furthermore $\widehat{DBE} = \widehat{DCE}$ (angles looking at the same arc on a cyclic quadrilateral), so triangles EBD and FCE are similar. We also have $\widehat{BED} = \widehat{BCD} = \widehat{DAB} = \widehat{CEF}$ . So, calling $DAB = \alpha$ , we have $\widehat{DBE} = \widehat{DCE} = \frac{\pi}{2} - \frac{\alpha}{2}$ . This way we get that $\widehat{ECG} = \frac{\pi}{2} - \frac{\alpha}{2}$ by difference of angles. So, angle $\widehat{FEG} = 2\alpha$ and $\widehat{EFG} = \widehat{EGF} = \frac{\pi}{2} - \alpha$ . So, we get

$\widehat{GAB} = \widehat{GFC} = \frac{\pi}{2} - \frac{\alpha}{2} - (\frac{\pi}{2} - \alpha) = \frac{\alpha}{2}$

and we are done.