Distinguishing cases, find the number of ordered triplets (x, y, z) of positive integers such that Let be the number of such triplets for n. We can get a first recursive formula by noticing that if and then . From this we deduce that as one can easily check that the cases where at least […]
Category: Maths
Seemingly Difficult, But Not Really
There are 12 red balls, 15 white balls and 17 black balls in a box. A person extracts all the balls, one at a time. What’s the probability that all the red balls will be extracted before the white balls and that all the white balls will be extracted before the black balls? There are […]
Inequality From Today’s Contest
Today a math contest I organized was held and I think this was the most difficult exercise overall. There are m distinct positive even integers and n distinct positive odd integers that add up to 1987. Find the maximum of 3m + 4n. So we have this sum of integers We can write that Now […]
Quarantine And Bijections
Now the majority of Italy is in lockdown again. So, why not spend some time doing combinatorics. Today’s subject is bashing sums without having to do any calculation. Let’s say we have this sum: One way to do it would be differentiating , then multiplying the result by x and differentiating again. Then we get […]
Cyclic Pentagon And Nice Angles
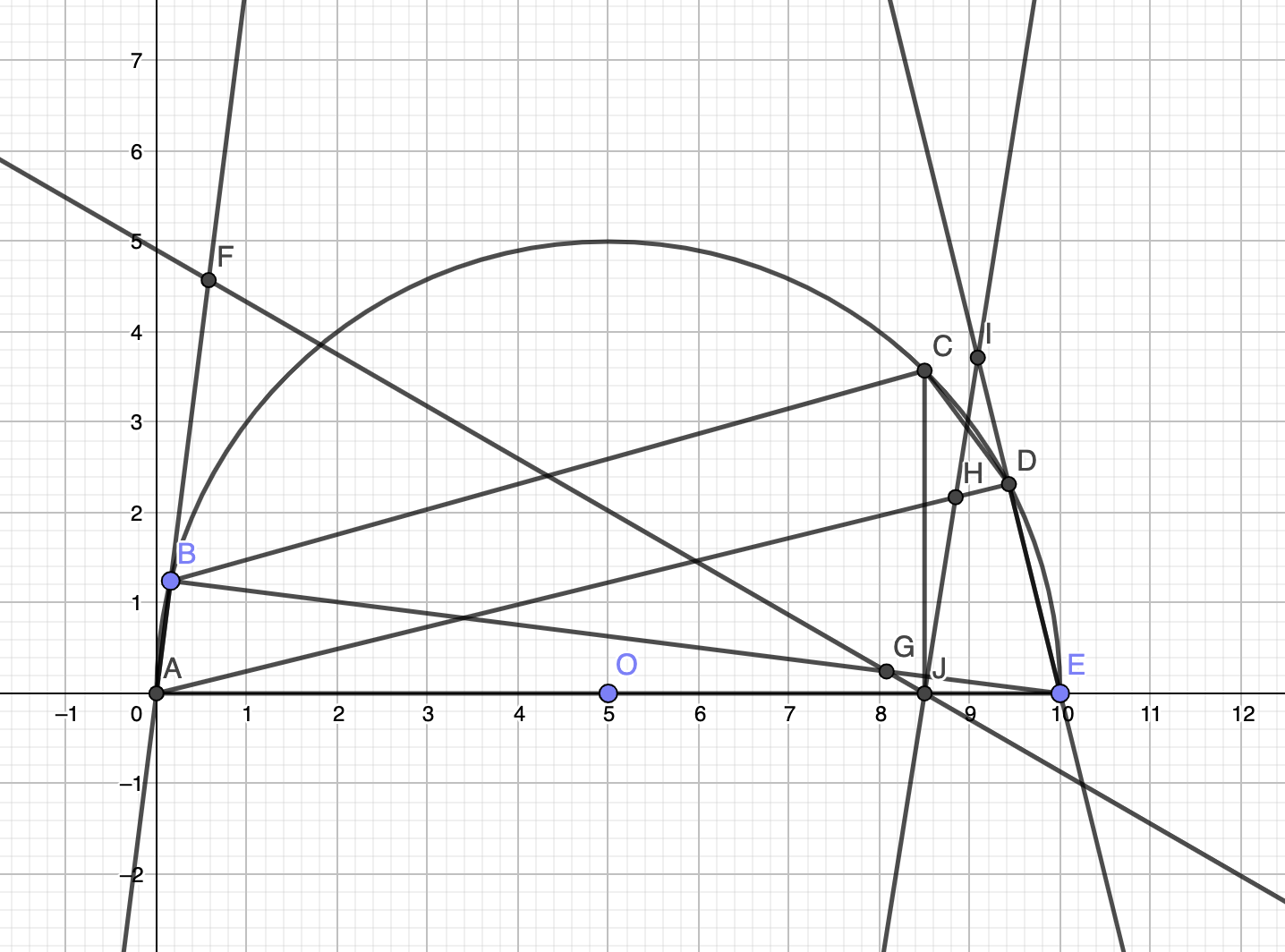
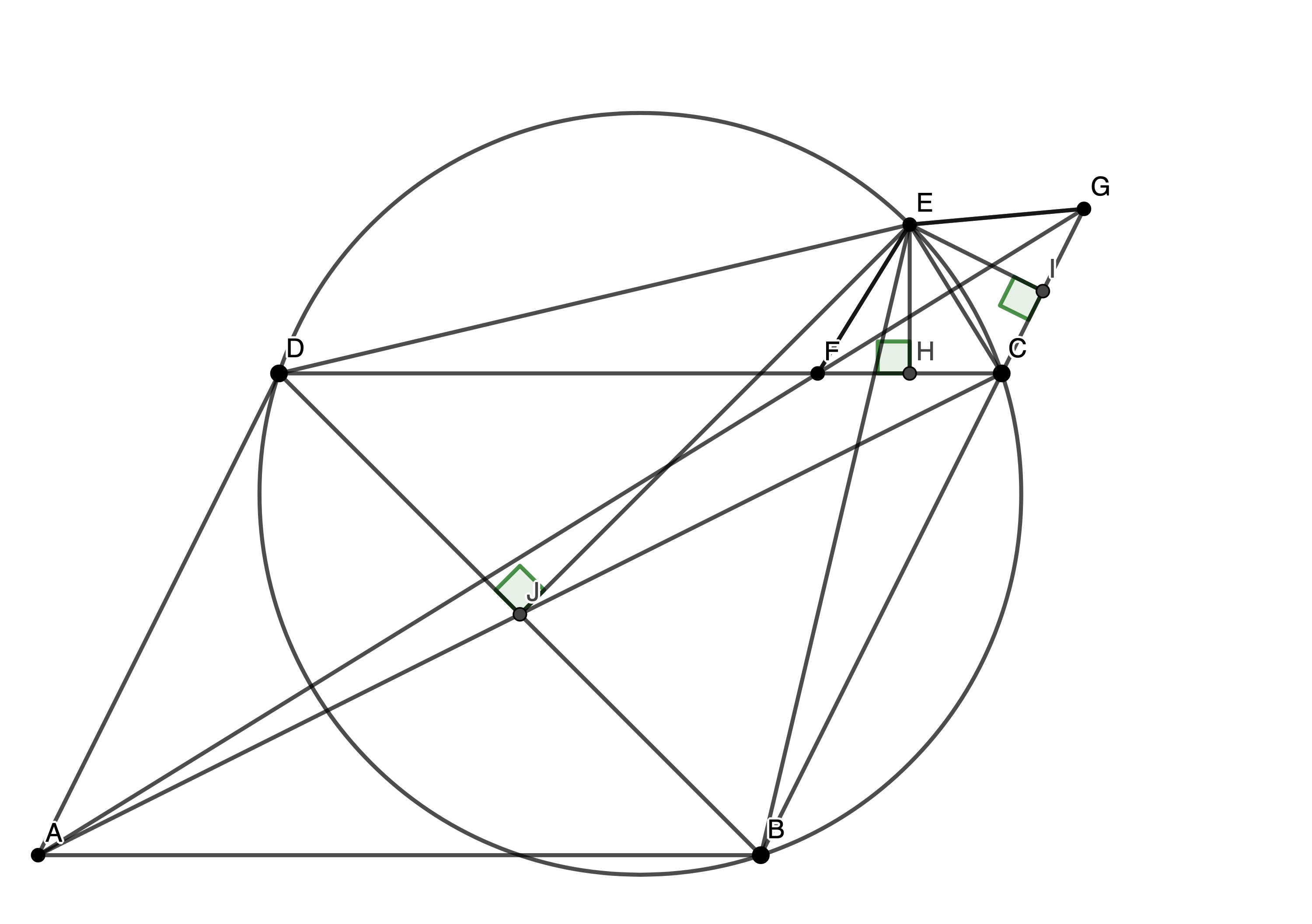
We have a cyclic pentagon, such that AE is a diameter and equals 10. We know and . Now F, G, H, I are the feet of the perpendiculars from C to AB, EB, AD, ED. If FG and HI concur at J, find FJI. Now, let K be the foot of the perpendicular from […]
Problem 7, Combinatorics
I proposed this problem in the last mathematical competition hosted on the Italian ‘gasmatematica’ website. The numbers from 000 to 999 must be put into some boxes, numbered from 00 to 99. If the label of a box is equal to a number with one digit removed, then the number can be put in that […]
Hidden Telescoping Sum
Here’s an exercise I proposed in an online competition. You have the following sequence: Find the integer part of: Now, notice that Hence By substitution, we have that the sum telescopes and reduces to Since is a very large number (the sequence has a quadratic increasing rate), we have that the integer part of the […]
IMO 2007/2
Consider five points A, B, C, D, E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that EF = EG = EC. Prove […]
An Application Of Burnside’s Lemma
Burnside’s Lemma is a very nice tool I had the occasion to use in the Mathematical Olympiads to solve some Combinatorics problems. It says that, given a finite group acting on a set , and, for each : let be the elements of invariant by . Then the number of orbits is equal to: May […]
A Constructive Combinatorics Proof
There is a positive integer in each square of a rectangular table. In each move, you may double each number in a row or subtract 1 from each number in a column. Can you arrive to a situation where there are only zeros on the table? How Should These Kind Of Problems Be Approached In […]