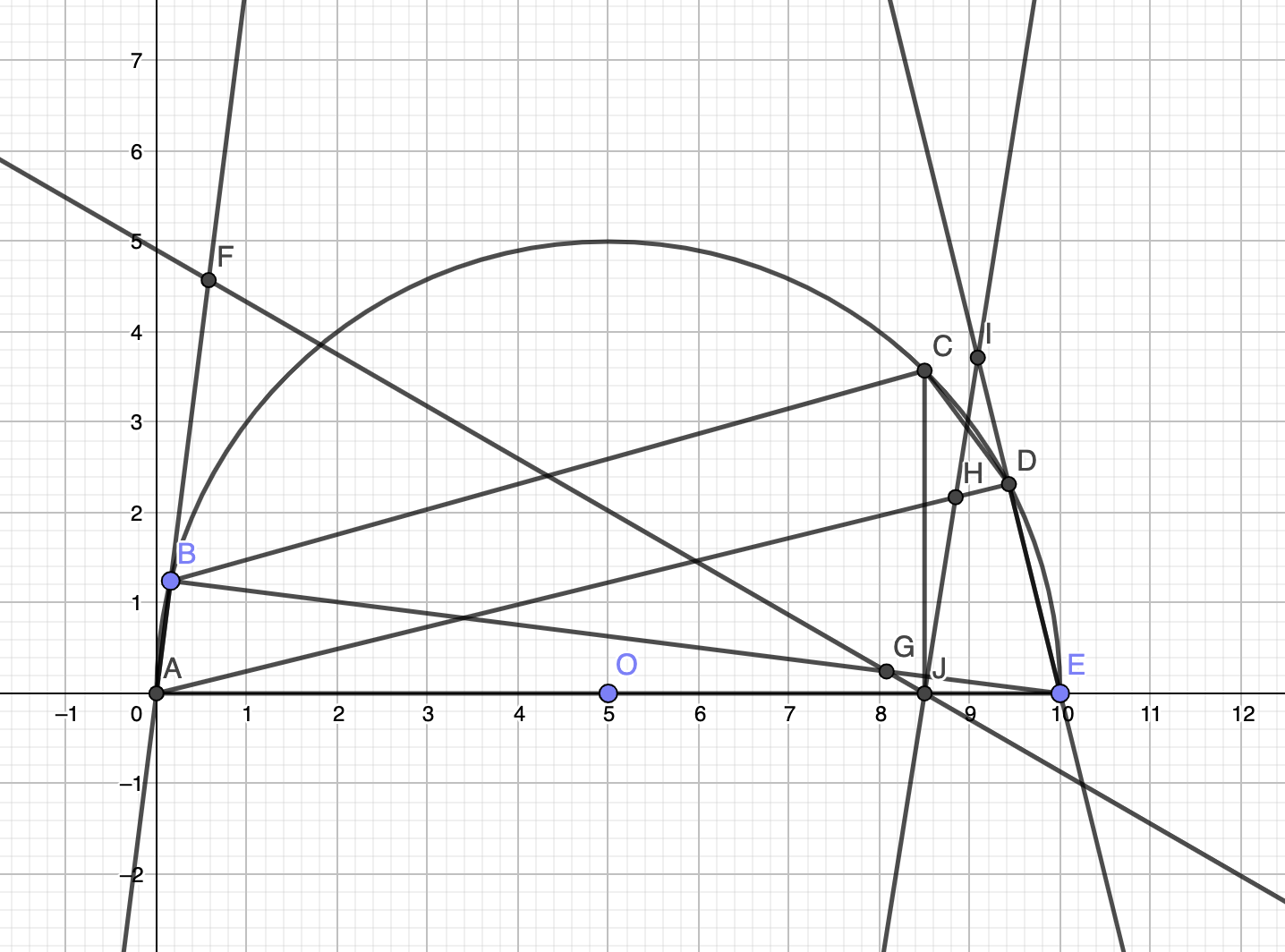
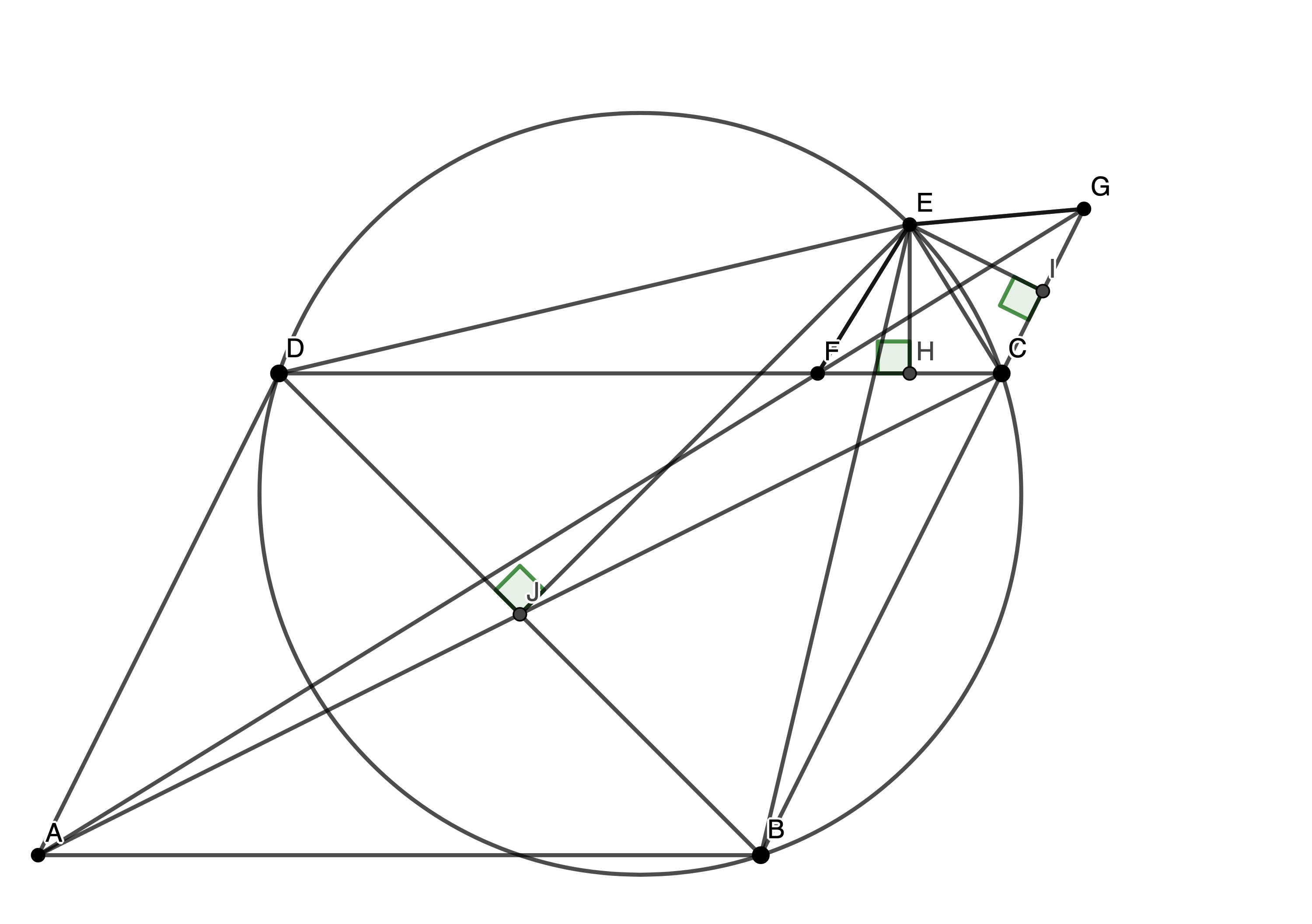
We have a cyclic pentagon, such that AE is a diameter and equals 10. We know and . Now F, G, H, I are the feet of the perpendiculars from C to AB, EB, AD, ED. If FG and HI concur at J, find FJI. Now, let K be the foot of the perpendicular from […]
Tag: SimsonLine
IMO 2007/2
Consider five points A, B, C, D, E such that ABCD is a parallelogram and BCED is a cyclic quadrilateral. Let l be a line passing through A. Suppose that l intersects the interior of the segment DC at F and intersects line BC at G. Suppose also that EF = EG = EC. Prove […]
Simson Lines In USA TST
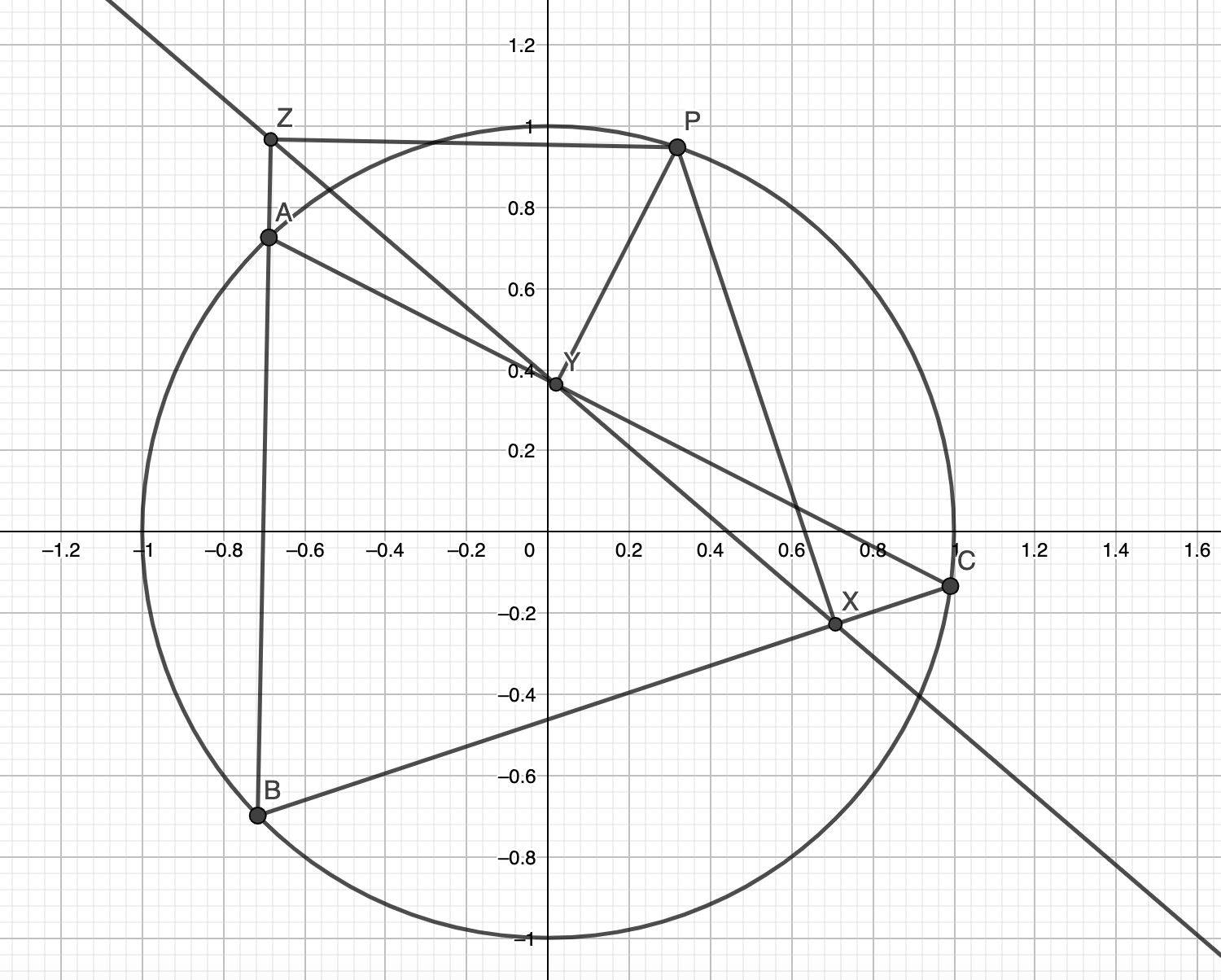
Given a point P on a triangle’s ABC’s circumcircle, then its projections on the sides of ABC are collinear (Simson Line). Using the notation from the figure above, notice that perpendiculars produce cyclic quadrilaterals: P is on the circumcircle of triangles YZA, ZXB and XYC. So we compute: due to all the cyclic quadrilaterals, and […]