Shortlist 2001/G1

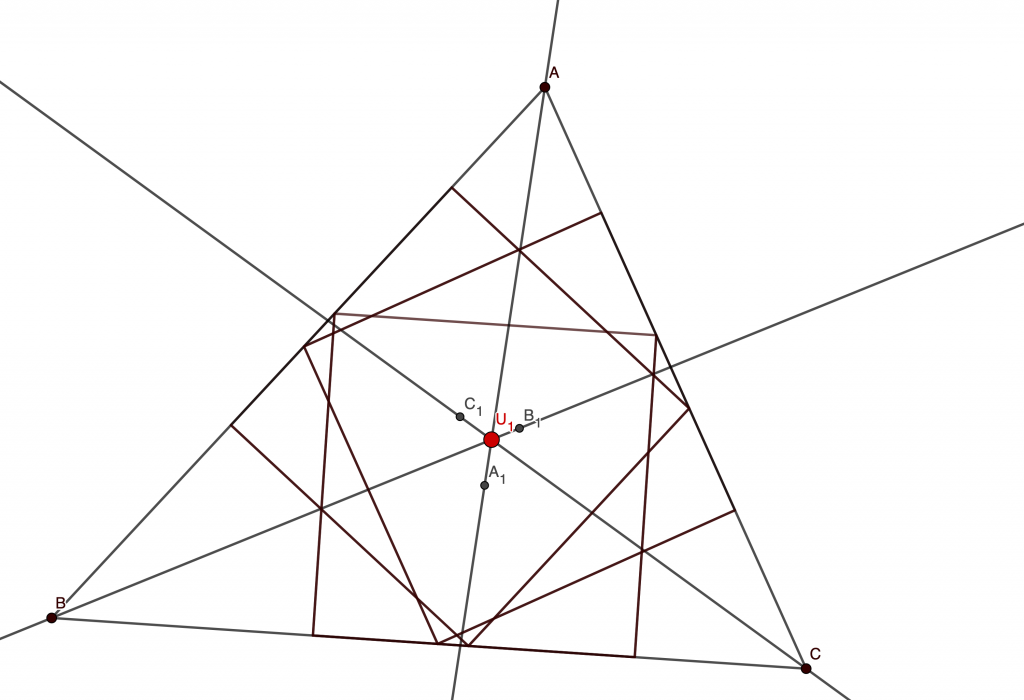
Let be the center of the square inscribed in acute triangle ABC with two vertices of the square on side BC. Thus one of the two remaining vertices of the square is on side AB and the other is on side BC. Points and are defined similarly. Prove that lines and are concurrent.

The Idea

Seen from this perspective, the problem may seem very hard, so the idea is to exploit a homothety bringing an inscribed square, say the one with two verticles on , to a square whose side coincides with .

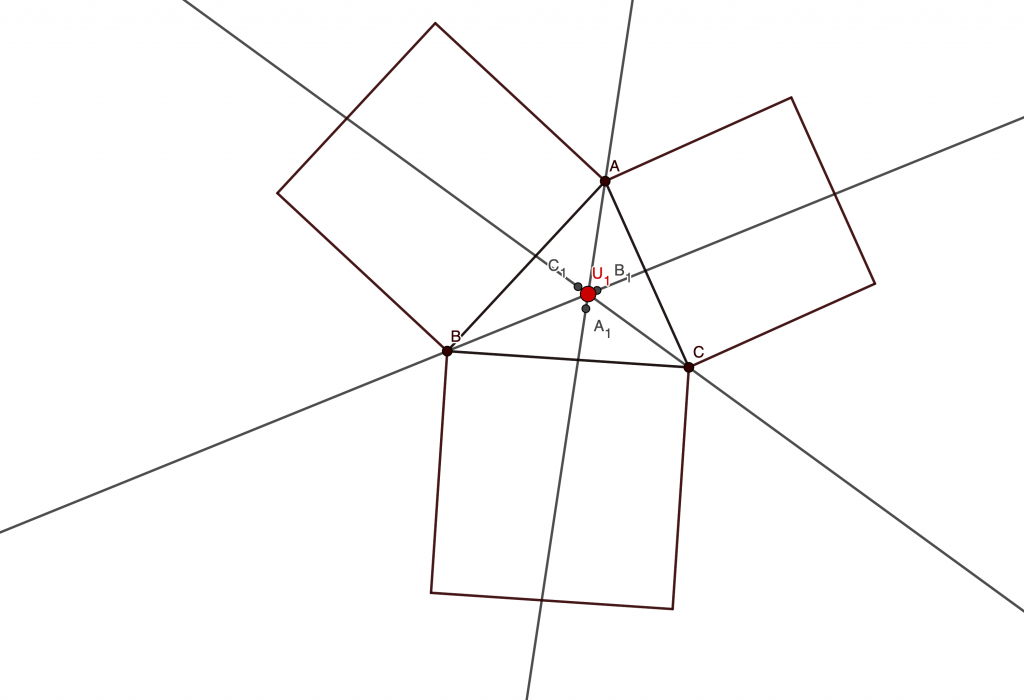
How do we show we can actually do it?

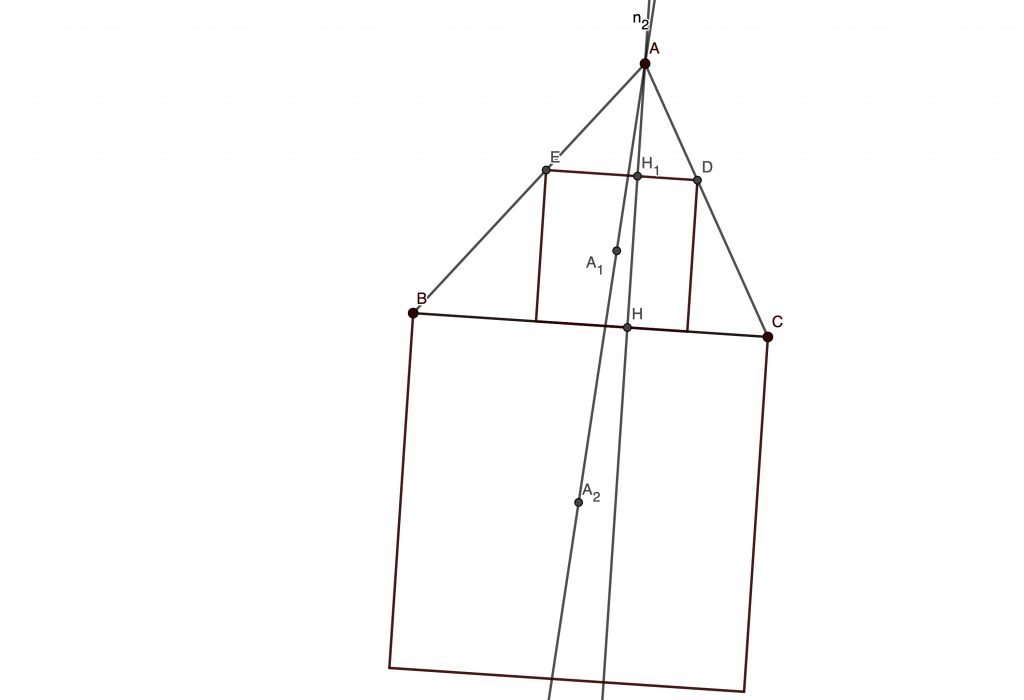
So there is a homothety with center A bringing to and to . So, because homothety preserves similarity and ratios, if we take the same homothety on the whole square, it will be sent to no other than the square constructed on with side . In particular, let be the center of the new square. Define and similarly.

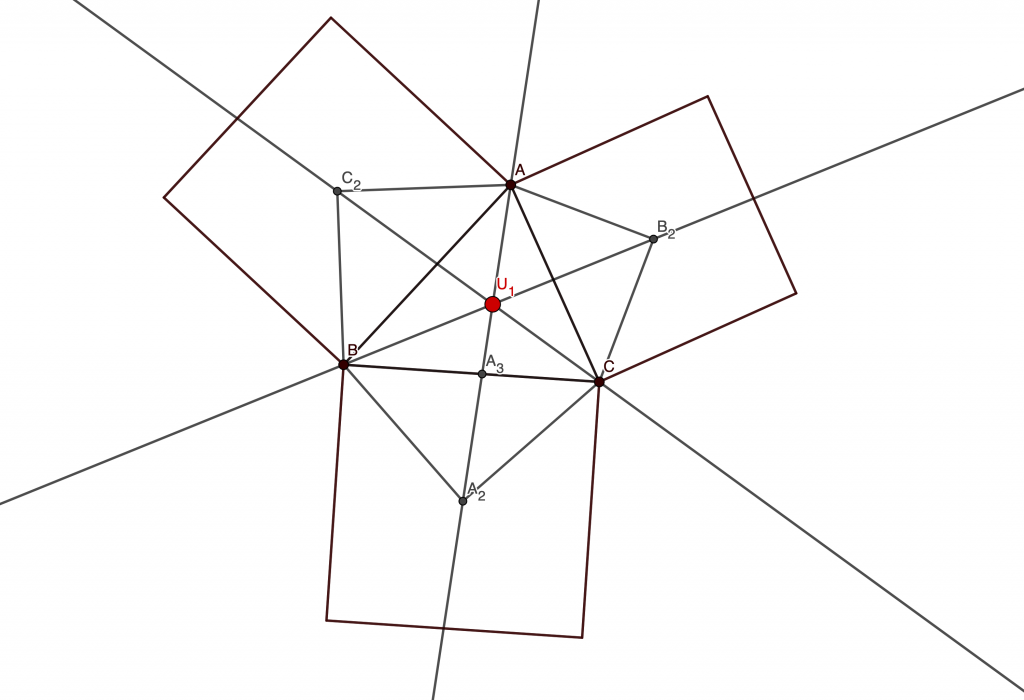
Now we see that considering line is equivalent to considering line and so on. So now we must show that lines concur. Now let’s use Ceva’s Theorem. Let be the intersection of line with . Define similarly. Now, by Ceva’s theorem, we have to show that

Looks very good for us, now the proof is pretty notorious and I will show it in the next part. It’s very educative to see how a seemingly horrifying problem can be turned into something easier with a wise use of homotheties.

Can you figure it out?

This is the end

Note that in standard notation, and, by replacing the areas with the standard area formula we obtain

since triangle is clearly hysosceles on base .
By analogous reasonings on the other sides of the triangle we obtain :