Happy 2021 everyone! As a way to start out the new year, what’s better than an article about the mathematical properties of the number 2021 to prepare for the next Mathematical Team Competitions? To start out, 2021 is not a prime number, its factorization is: Hence, be prepared for a lot of chinese remainder theorem […]
Category: Maths
A Problem From Stanford Mathematics Tournament 2008 (Team Test)
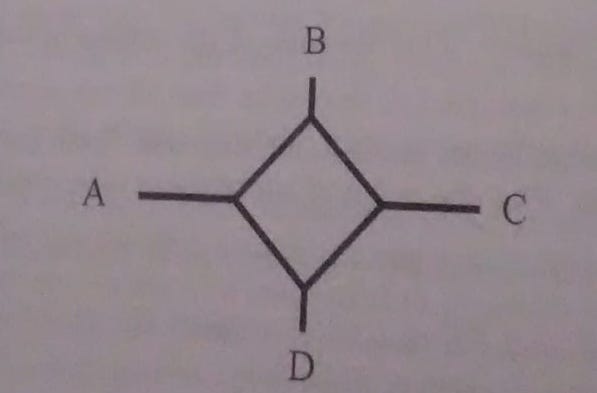
Daphne is in a maze of tunnels shown below. She enters at A, and at each intersection, chooses a direction randomly (including possibly turning around). Once Daphne reaches an exit, she will not return into the tunnels. What is the probability that she will exit at A? The Idea At first, I will denote by […]
Shortlist 2001/G1
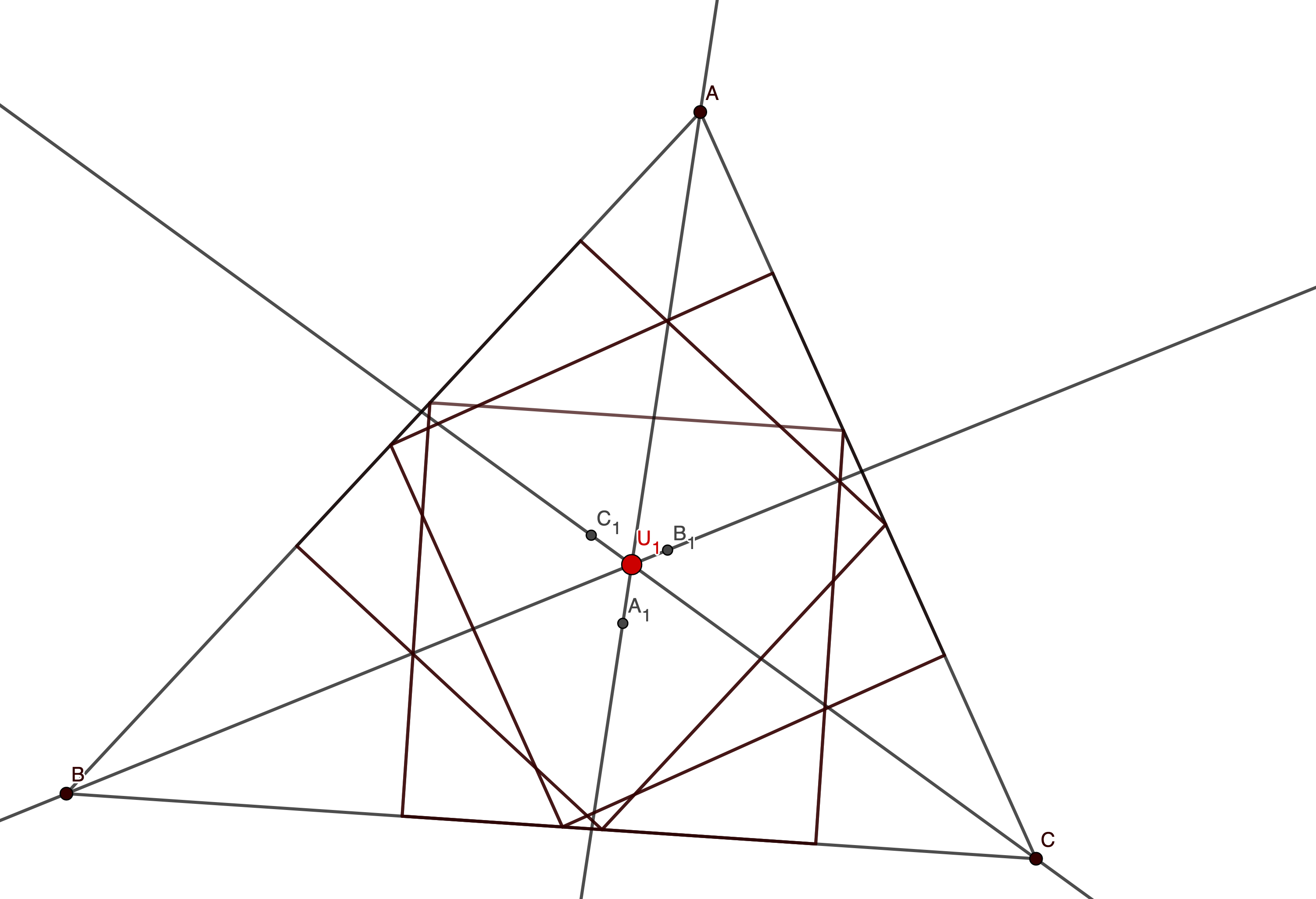
Let be the center of the square inscribed in acute triangle ABC with two vertices of the square on side BC. Thus one of the two remaining vertices of the square is on side AB and the other is on side BC. Points and are defined similarly. Prove that lines and are concurrent. The Idea […]
Algebra At Christmas
Why not? I mean, it’s a nice inequality to try out. What if I asked you to find the maximum value of Well, time to apply the AM-GM inequality. First, let’s say that Notice that by the AM-GM inequality applied on the 4 positive real numbers Hence, we get that with equality when
Shortlist 2006/A5
Let be the sides of a triangle. Prove that Always Try A Substitution We notice that the denominators are all positive, in fact by the triangular inequality. So let . Then . So we get applying in the last step. Similarly, we obtain Thus, now it is sufficient to prove that So let’s assume WLOG […]
IMO 2019/4
Find all couples of integers which satisfy The Idea We notice that work and we claim that other solutions don’t exist, so we want to get an upper and lower bound for . Proof Now let be the greatest exponent of prime in the scomposition of , we notice that and . Hence, Now we […]
Combinatorial Extremization
The best combinatorics book I’ve read so far is ‘Combinatorial Extremization’, by Yuefeng Feng. The book is divided into 13 chapters. Each of them covers a particular combinatorial technique you can use to solve your problems. Some of them are easy to understand, but in general, the level of difficulty of this book is quite […]
Problem Solving Through Problems
One of the best mathematics book I’ve ever read is ‘Problem-Solving Through Problems’, by Loren C. Larson. The book is composed of 8 chapters. Each of these talks about a certain mathematical tool or topic. After a brief theory introduction, shows a lot of interesting example problems, which are very instructional and show how you […]
Euclidean Geometry In Mathematical Olympiads, Evan Chen
The most complete and interesting Geometry theory book I’ve ever read is ‘Euclidean Geometry In Mathematical Olympiads’, by Evan Chen. We could say that it’s the Bible of people who love Geometry problems in the Olympiads. It is divided into 10 theory chapters, which talk about different branches and techniques you can use to solve […]
Problem Solving Strategies
A very interesting non-calculus mathematics book is ‘Problem-Solving Strategies’, by Arthur Engel. It gathers competition problems from over twenty national and international competitions of high school students. The book is composed of 14 chapters. Each of these explains a particular mathematical concept, like the Extremal Principle, shows some exercises with solutions and then proposes some […]