In this article, I’ll show you five different equations you can use to plot your own heart.
Let’s start with the simplest:
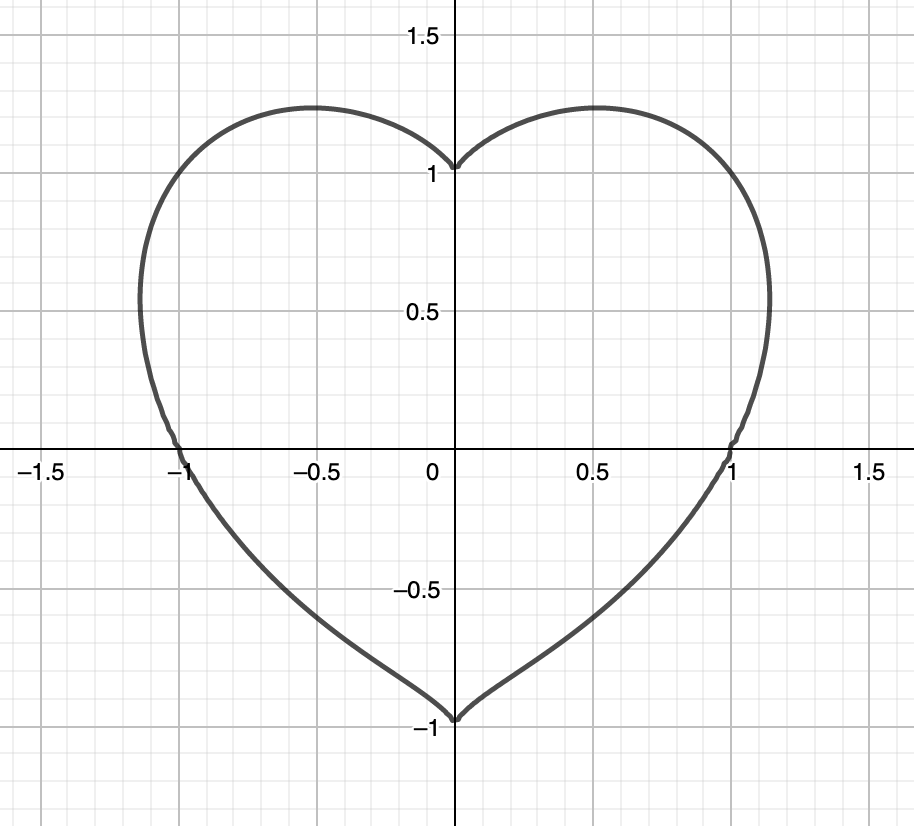
I think this is the most classic of the five I’m going to show you.
If you prefer one which is a little bit thinner, there is this one:
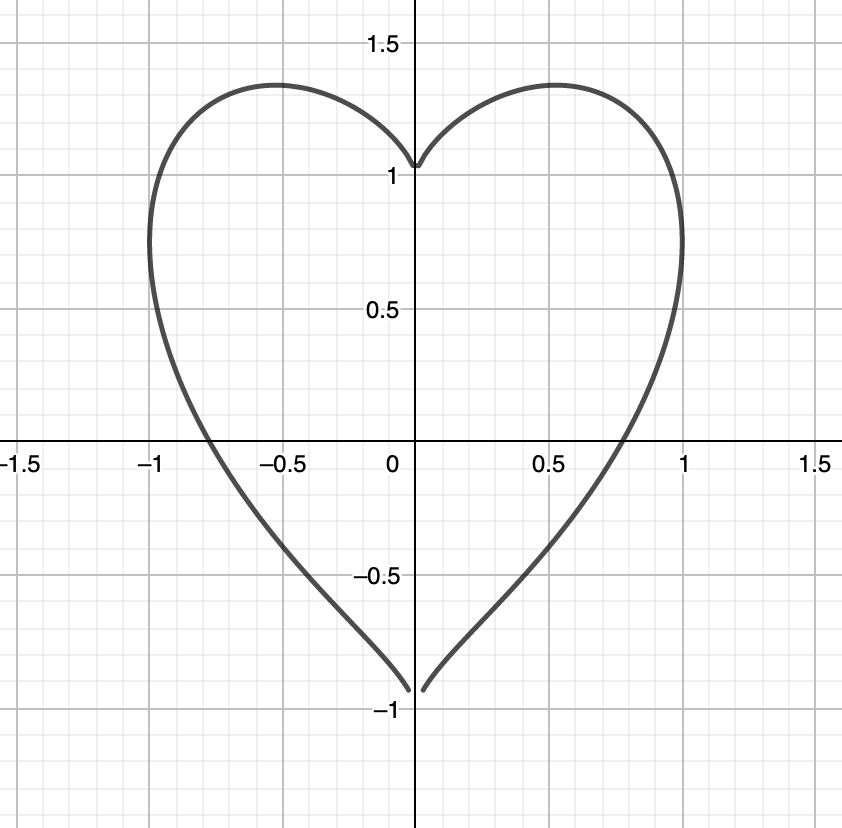
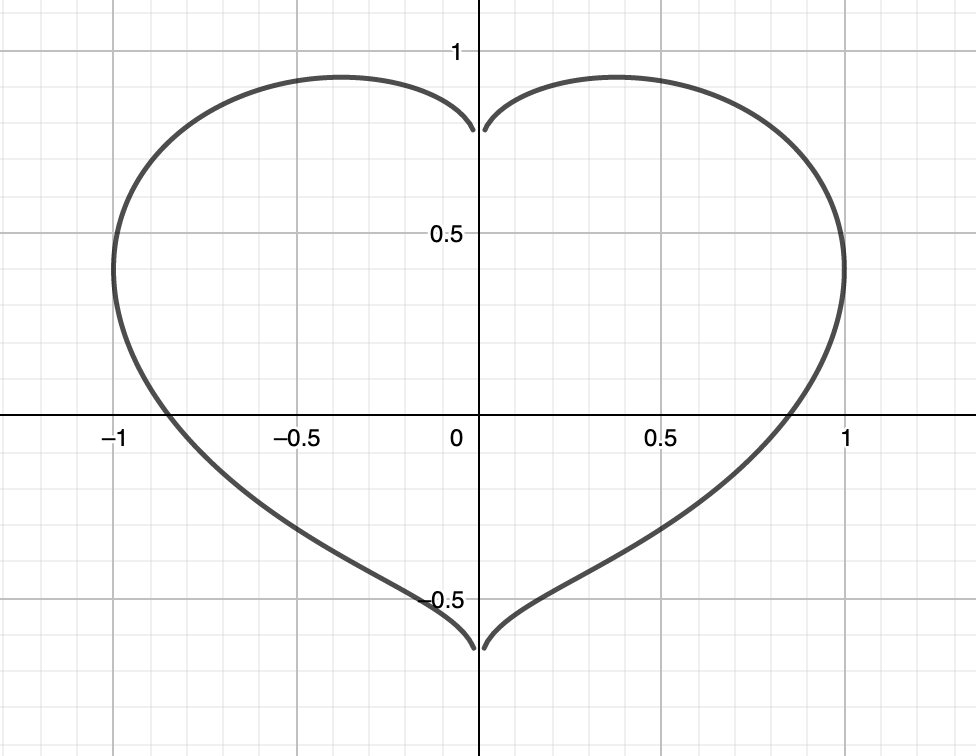
On the other hand, there is also one that is fatter:
Python Implementation For Plotting Two Parametric Hearts
To plot the hearts, I’m using the numpy and matplotlib libraries of Python.
The first parametric equation is:
Where
Its code implementation is:
import numpy as np
import matplotlib.pyplot as plt
def heart_plotter(precision):
t = np.linspace(0, 60, precision)
X = 1/100*(-t**2 + 40*t + 1200)*np.sin(t/90)
Y = 1/100*(-t**2 + 40*t + 1200)*np.cos(t/60)
Y_1 = 1/100*(-t**2 + 40*t + 1200)*np.cos(t/60)
X_1 = -1/100*(-t**2 + 40*t + 1200)*np.sin(t/90)
X = np.concatenate((X, np.flip(X_1)))
Y = np.concatenate((Y, np.flip(Y_1)))
return X, Y
x, y = heart_plotter(1000)
plt.plot(x, y, c='r')
plt.show()
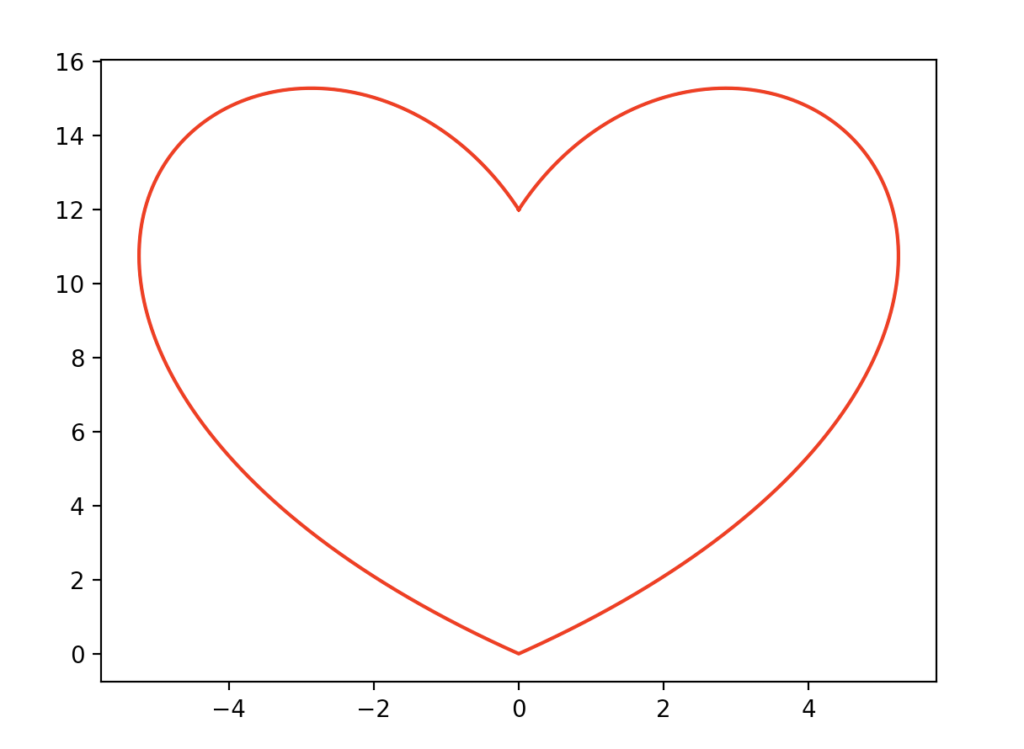
A very classic shape. As you can see it’s very easy to perform calculations with numpy arrays and its builtin functions.
Warning: if you don’t reverse the order of the arrays before concatenating (np.flip), the line x=0 would appear in the plot connecting the two ‘cusps’ of the heart, because the plot function of matplotlib would think there’s a gap in the graph of the equation.
The second parametric equation is the one I prefer:
Where
Its code implementation is:
import numpy as np
import matplotlib.pyplot as plt
def heart_plotter(precision):
t = np.linspace(-1, 1, 2*precision+1)
X = np.sin(t)*np.cos(t)*np.log(np.abs(t))
Y = np.sqrt(np.abs(t))*np.cos(t)
return X, Y
x, y = heart_plotter(1000)
plt.plot(x, y, c='r')
plt.show()
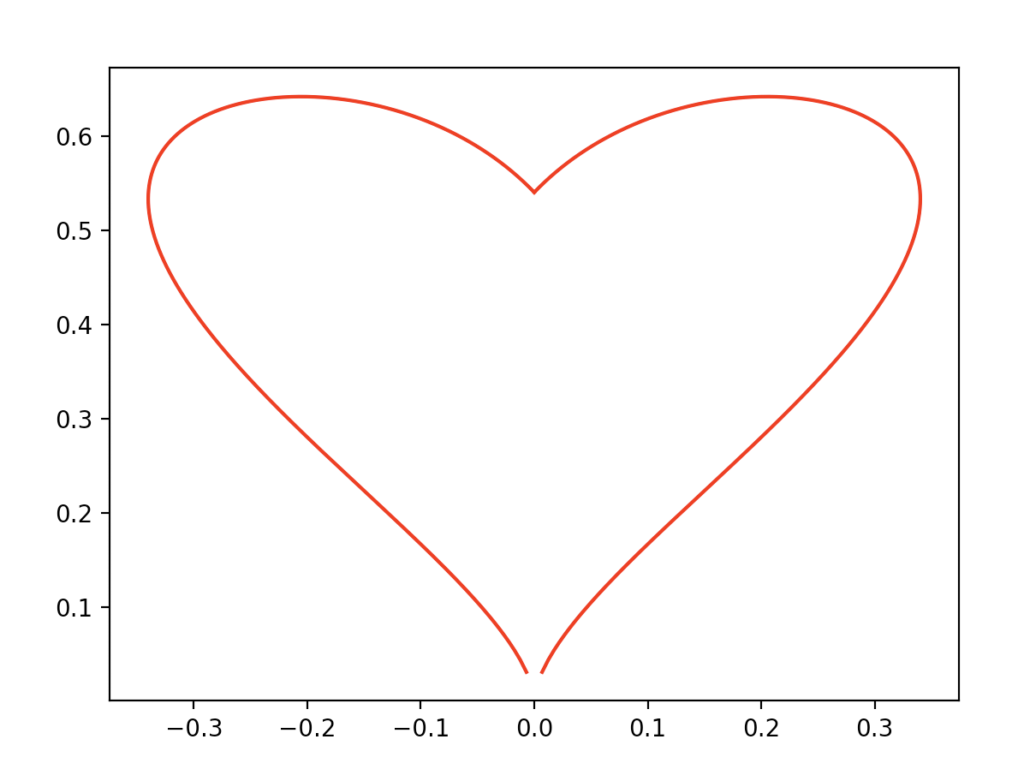
I really like the shape of this heart, it seems like it’s constantly expanding.
I’m using 2*precision + 1 because, this way, there is that little gap near 0. If precision was even, there would be a line joining the two borders, which is not very aesthetically pleasing.